如图7,在平面直角坐标系xOy中,一抛物线的顶点坐标是(0,1),且过点(-2,2),平行四边形OABC的顶点A、B在此抛物线上,AB与y轴相交于点M.已知点C的坐标是(-4,0),点Q(x,y)是抛物线上任意一点.
(1) 求此抛物线的解析式及点M的坐标;
(2) 在x轴上有一点P(t,0),若PQ∥CM,试用x的代数式表示t;
(3) 在抛物线上是否存在点Q,使得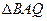 的面积是
的面积是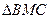 的面积的2倍?若存在,求
的面积的2倍?若存在,求
此时点Q的坐标.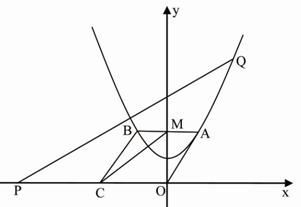
相关知识点
推荐套卷
如图7,在平面直角坐标系xOy中,一抛物线的顶点坐标是(0,1),且过点(-2,2),平行四边形OABC的顶点A、B在此抛物线上,AB与y轴相交于点M.已知点C的坐标是(-4,0),点Q(x,y)是抛物线上任意一点.
(1) 求此抛物线的解析式及点M的坐标;
(2) 在x轴上有一点P(t,0),若PQ∥CM,试用x的代数式表示t;
(3) 在抛物线上是否存在点Q,使得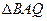 的面积是
的面积是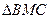 的面积的2倍?若存在,求
的面积的2倍?若存在,求
此时点Q的坐标.