设集合A={0,1,2}，B={0,1,2}，分别从集合A和B中随机 取一个数a,和b，确定平面上的一个点P(a,b)，记“点P(a,b)落在直线x+y=n上”为事件Cn(0≤n≤4， n∈N)，若事件Cn的概率最大，则n的可能值为 。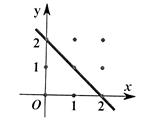
的最小正周期为 ．
，
，
，若
，则
．
”的否定是 ．
，
，则
．
，则使得
成立的
的取值范围为_______．推荐套卷
设集合A={0,1,2}，B={0,1,2}，分别从集合A和B中随机 取一个数a,和b，确定平面上的一个点P(a,b)，记“点P(a,b)落在直线x+y=n上”为事件Cn(0≤n≤4， n∈N)，若事件Cn的概率最大，则n的可能值为 。
粤公网安备 44130202000953号