（本小题满分7分）如图，已知二次函数
的图象与x轴负半轴交于点A（-1，0），与y轴正半轴交与点B，顶点为P，且OB=3OA，一次函数y=kx+b的图象经过A、B．
（1）求一次函数解析式；
（2）求顶点P的坐标；
（3）平移直线AB使其过点P，如果点Ｍ在平移后的直线上，且
，求点M坐标；
（４）设抛物线的对称轴交x轴与点E，联结AP交y轴与点D，若点Q、N分别为两线段PE、PD上的动点，联结QD、QN，请直接写出QD+QN的最小值．
相关试题
甲乙两车间生产一种产品，原计划两车间共生产300件产品，实际甲车
间比原计划多生产10%，乙车间比原计划多生产20%，结果共生产了340
件产品，问原计划甲、乙两车间各生产了多少件产品？
已知:∠B=∠2, ∠1=30°,求∠D
完成填空
解：∵∠2=∠B（已知）
∴AD//BC ( )
∴∠D=∠1 ( )
又∵∠1=30°
∴∠D=30° （等量代换）
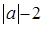=9是关于x、y的二元一次方程，求a值。
相关知识点
推荐套卷
粤公网安备 44130202000953号