（本小题满分12分）
已知函数
（Ⅰ）若曲线y=
f(x)在点P（1，f(1)）处的切线与直线y=x+2垂直，求函数y=f(x)的单调区间；
（Ⅱ）若对于任意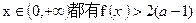
成立，试求a的取值范围；
（Ⅲ）记g(x)=f(x)+x-b(b∈R).当a=1时，函数g(x)在区间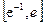
上有两个零点，求实数b的取值范围。
相关试题
，不等式
的解集是
．
； 
时，求函数
．
．
在
上是减函数；
上的单调性（无需证明）；
上的值域是
，求
的最大值和最小值．
经过点
．
的值；
图象，并写出该函数在
上的单调区间．
； 
，
．
；（2）
．推荐套卷
（本小题满分12分）
已知函数
（Ⅰ）若曲线y=f(x)在点P（1，f(1)）处的切线与直线y=x+2垂直，求函数y=f(x)的单调区间；
（Ⅱ）若对于任意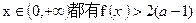成立，试求a的取值范围；
（Ⅲ）记g(x)=f(x)+x-b(b∈R).当a=1时，函数g(x)在区间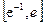上有两个零点，求实数b的取值范围。
粤公网安备 44130202000953号