本题共有3个小题,第1小题满分5分,第2小题满分6分,第3小题满分7分
已知曲线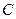 的方程为
的方程为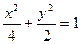 ,
,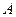 、
、 为曲线上的两点,
为曲线上的两点, 为坐标原点,且有
为坐标原点,且有 .
.
(1)若 所在直线的方程为
所在直线的方程为 ,求
,求 的值;
的值;
(2)若点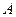 为曲线
为曲线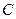 上任意一点,求证:
上任意一点,求证: 为定值;
为定值;
(3)在(2)的基础上,用类比或推广的方法对新的圆锥曲线 写出一个命题,并对该命题加以证明.
写出一个命题,并对该命题加以证明.
推荐套卷
本题共有3个小题,第1小题满分5分,第2小题满分6分,第3小题满分7分
已知曲线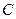 的方程为
的方程为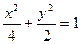 ,
,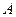 、
、 为曲线上的两点,
为曲线上的两点, 为坐标原点,且有
为坐标原点,且有 .
.
(1)若 所在直线的方程为
所在直线的方程为 ,求
,求 的值;
的值;
(2)若点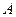 为曲线
为曲线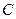 上任意一点,求证:
上任意一点,求证: 为定值;
为定值;
(3)在(2)的基础上,用类比或推广的方法对新的圆锥曲线 写出一个命题,并对该命题加以证明.
写出一个命题,并对该命题加以证明.