(本小题满分13分)
设点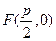 (
(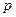 为正常数),点
为正常数),点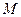 在
在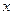 轴的负半轴上,点
轴的负半轴上,点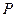 在
在 轴上,且
轴上,且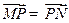 ,
, .
.
(Ⅰ)当点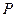 在
在
 轴上运动时,求点
轴上运动时,求点 的轨迹
的轨迹 的方程;
的方程;
(Ⅱ)直线 过点
过点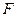 且与曲线
且与曲线 相交于不同两点
相交于不同两点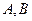 ,分别过点
,分别过点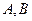 作直线
作直线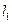 :
: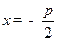 的
的 垂线,对应的垂足分别为
垂线,对应的垂足分别为
 ,求
,求 的值;
的值;
(Ⅲ)在(Ⅱ)的条件下,记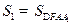 ,
, ,
,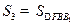 ,
,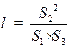 ,求
,求 的值.
的值.
推荐套卷
(本小题满分13分)
设点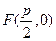 (
(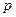 为正常数),点
为正常数),点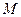 在
在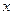 轴的负半轴上,点
轴的负半轴上,点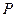 在
在 轴上,且
轴上,且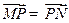 ,
, .
.
(Ⅰ)当点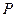 在
在
 轴上运动时,求点
轴上运动时,求点 的轨迹
的轨迹 的方程;
的方程;
(Ⅱ)直线 过点
过点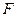 且与曲线
且与曲线 相交于不同两点
相交于不同两点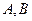 ,分别过点
,分别过点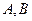 作直线
作直线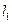 :
: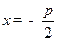 的
的 垂线,对应的垂足分别为
垂线,对应的垂足分别为
 ,求
,求 的值;
的值;
(Ⅲ)在(Ⅱ)的条件下,记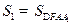 ,
, ,
,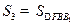 ,
,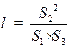 ,求
,求 的值.
的值.