从装有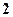 个红球,
个红球,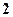 个白球和
个白球和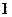 个黑球的袋中逐一取球,已知
个黑球的袋中逐一取球,已知 每个球被抽取的可能性相同.
每个球被抽取的可能性相同.
(1)若抽取后又放回,抽取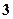 次,分别求恰有
次,分别求恰有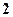 次是红球的概率及抽全三种颜色球的概率;
次是红球的概率及抽全三种颜色球的概率;
(2)若抽取后不放回,求抽完红球所需次数不少于4次的概率;
(3)记红球、白球、黑球对应的号码为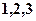 ,现从盒中有放回地先后抽出的两球的号码分别记
,现从盒中有放回地先后抽出的两球的号码分别记
为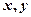 ,记
,记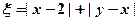 ,求随机变量
,求随机变量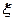 的分布列.
的分布列.
推荐套卷
从装有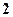 个红球,
个红球,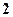 个白球和
个白球和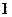 个黑球的袋中逐一取球,已知
个黑球的袋中逐一取球,已知 每个球被抽取的可能性相同.
每个球被抽取的可能性相同.
(1)若抽取后又放回,抽取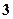 次,分别求恰有
次,分别求恰有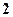 次是红球的概率及抽全三种颜色球的概率;
次是红球的概率及抽全三种颜色球的概率;
(2)若抽取后不放回,求抽完红球所需次数不少于4次的概率;
(3)记红球、白球、黑球对应的号码为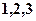 ,现从盒中有放回地先后抽出的两球的号码分别记
,现从盒中有放回地先后抽出的两球的号码分别记
为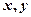 ,记
,记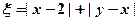 ,求随机变量
,求随机变量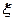 的分布列.
的分布列.