学校欲在操场边上一直角三角形空地ABC上种植草坪，并需铺设一根水管EF（E在AC上，F在AB上）用于灌溉，已知∠A=30°，∠C=90°，BC=2a
，D是BC中点，为确保灌溉的效果，铺设时要求∠EDF=
60°。现有两种方案可供参考。甲方案：取AC的中点E铺设水管；乙方案：取AB的中点F铺设水管。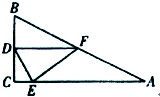
（1）比较甲乙两种方案，哪一种方案更合理（EF的长较小的合理）；
（2）学校研究小组通过研究得出：无论D在BC的什么位置，总存在E，F两点，使△DEF为正三角形
。试证明该结论的正确性。
相关试题
中，
为角平分线，
为
交
于
，若
，
且
，
，用
、
表示
，
，
m]
（
，
）
的值域；
，且
的最小值为
，求
．
的单调区间；
恒成立，试确定实数k的取值范围；
．
，若
且
，
在
内有最大值无最小值．
中，
、
、
分别是角A、B、C的对边，
，其面积
，求
已知数列{an}，a1＝1，an＝λan－1＋λ－2（n≥2）．相关知识点
推荐套卷
粤公网安备 44130202000953号