已知动点P与双曲线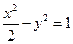
的两个焦点F1，F2的距离之和为定值，
且cos∠F1PF2的最小值为－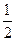
.
（1）求动点P的轨迹方程；
（2）是否存在直线l与P点轨迹交于不同的两点M、N，且线段MN恰被直线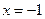
平分？若存在，求出直线l的斜率k的取值范围，若不存在说明理由.
相关试题
（2）
，若存在闭区间
和常数
，使得对任意
，都有
，且对任意
∈D，当
时，
恒成立，则称函数
和
是否为R上的“平底型”函数？并说明理由；
对一切
R恒成立，求实数
的取值范围；
是区间
上的“平底型”函数，求
和
的值．相关知识点
推荐套卷
已知动点P与双曲线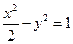的两个焦点F1，F2的距离之和为定值，
且cos∠F1PF2的最小值为－.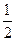
（1）求动点P的轨迹方程；
（2）是否存在直线l与P点轨迹交于不同的两点M、N，且线段MN恰被直线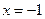平分？若存在，求出直线l的斜率k的取值范围，若不存在说明理由.
粤公网安备 44130202000953号