（本小题满分12分）
将边长为2的正方形ABCD沿对角线BD折叠，使得平面ABD⊥平面CBD，AE⊥平面ABD，且AE＝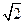
．
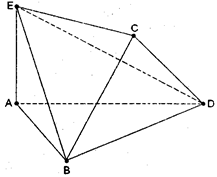
（Ⅰ）求证：DE⊥AC；
（Ⅱ）求DE与平面BEC所成角的正弦值；
（Ⅲ）直线BE上是否存在一点M，使得CM∥平面ADE，若存在，求点M的位置，不存在请说明理由．
，
:
,
:
．
的取值范围；
，“
的取值范围
时，求函数
的最小值
是定义在
的增函数，
,求
的取值范围
在
单调递增
推荐套卷
（本小题满分12分）
将边长为2的正方形ABCD沿对角线BD折叠，使得平面ABD⊥平面CBD，AE⊥平面ABD，且AE＝．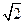
（Ⅰ）求证：DE⊥AC；
（Ⅱ）求DE与平面BEC所成角的正弦值；
（Ⅲ）直线BE上是否存在一点M，使得CM∥平面ADE，若存在，求点M的位置，不存在请说明理由．
粤公网安备 44130202000953号