(8分).
一个多面体的直观图和三视图如图所示，其中M、N分别是AB、AC的中点，G是DF上的一动点.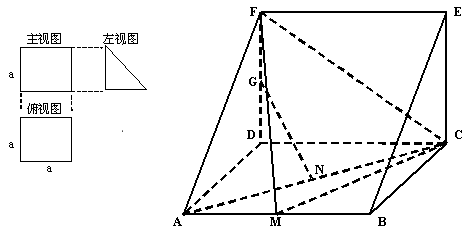
( 1) 求该多面体的体积.
（2）求证：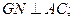
（3）当FG=GD时，在棱AD上确定一点P，使得GP//平面FM
C,并给出证明.
相关试题
且
在
处取得极小值.
在
上是增函数，求实数
的取值范围。
中，
的前n项和，
，数列
的前n项和为
求(本题满分14分)在锐角三角形ABC中，已知角A、B、C所对的边分别为a、b、c，且
，
（1）若c2＝a2＋b2—ab，求角A、B、C的大小；
（2）已知向量
的取值范围。
．
的单调递增区间；
，
，求
的值．
的各项均为正数，前
项和为
，且
…
，求
。推荐套卷
(8分).
一个多面体的直观图和三视图如图所示，其中M、N分别是AB、AC的中点，G是DF上的一动点.
( 1) 求该多面体的体积.
（2）求证：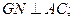
（3）当FG=GD时，在棱AD上确定一点P，使得GP//平面FMC,并给出证明.
(本题满分14分)在锐角三角形ABC中，已知角A、B、C所对的边分别为a、b、c，且，
（1）若c2＝a2＋b2—ab，求角A、B、C的大小；
（2）已知向量的取值范围。
粤公网安备 44130202000953号