．
设y="A" sin(ωx+j)(A＞0，ω＞0，|j|＜π)最高点D的坐标为（2，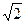
），由
最高点运动到相邻的最低点时，曲线与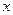
轴交点E的坐标为(6，0)，(1)求A、ω、j的值；(2)求出该函数的频率，初相和单调区间．
推荐套卷
．
设y="A" sin(ωx+j)(A＞0，ω＞0，|j|＜π)最高点D的坐标为（2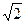，），由最高点运动到相邻的最低点时，曲线与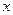轴交点E的坐标为(6，0)，(1)求A、ω、j的值；(2)求出该函数的频率，初相和单调区间．
粤公网安备 44130202000953号