设函数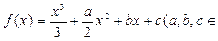
R)，函数
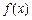的导数记为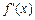
.
（1）若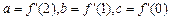
，求a、b、c的值；
（2）在（1）的条件下，记
，求证：F(1)+ F(2)+ F(3)+…+ F(n)<
N*);
（3）设关于x的方程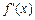=0的两个实数根为α、β，且1<α<β<2.试问：是否存在正整数n0，使得
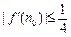？说明理由.
推荐套卷
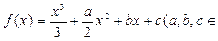设函数R)，函数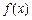的导数记为.
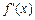（1）若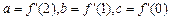，求a、b、c的值；
（2）在（1）的条件下，记，求证：F(1)+ F(2)+ F(3)+…+ F(n)<N*);
（3）设关于x的方程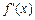=0的两个实数根为α、β，且1<α<β<2.试问：是否存在正整数n0，使得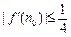？说明理由.
粤公网安备 44130202000953号