(本小题满分12分)
某校选拔 若干名学生组建数学奥林匹克集训队,要求选拔过程分前后两次进行,当第一次选拔合格后方可进入第二次选拔,两次选拔相互独立。根据甲、乙、丙三人现有的水平,第一次选拔,甲、乙、丙三
若干名学生组建数学奥林匹克集训队,要求选拔过程分前后两次进行,当第一次选拔合格后方可进入第二次选拔,两次选拔相互独立。根据甲、乙、丙三人现有的水平,第一次选拔,甲、乙、丙三 人合格的概率依次为0.5、0.6、0.4,第二次选拔,甲、乙、丙三人合格的概率依次为0.6、0.5、0.5。
人合格的概率依次为0.5、0.6、0.4,第二次选拔,甲、乙、丙三人合格的概率依次为0.6、0.5、0.5。
(I)求第一次选拔后甲、乙两人中只有甲合格,而乙不合格的概率;
(II)分别求出甲、乙、丙三人经过前后两次选拔后合格入选的概率;
(III)设经过前后两次选拔后合格入选的人数为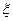 ,求
,求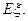
推荐套卷



 面积的最小值。
面积的最小值。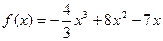
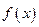 的单调区间和值域;
的单调区间和值域;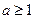 ,函数
,函数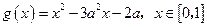 ,若对于任意
,若对于任意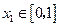 ,总存在
,总存在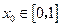 ,
, 成立,求
成立,求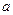 的取值范围
的取值范围

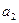
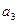

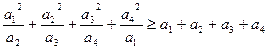
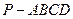


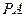





 ;
; (2)若
(2)若 为
为 上的动点,
上的动点,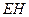 与平面
与平面 所成最大角的正切值为
所成最大角的正切值为 ,求锐二面角
,求锐二面角 的余弦值;
的余弦值; ,求点
,求点 到平面
到平面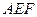 的距离。
的距离。 粤公网安备 44130202000953号
粤公网安备 44130202000953号