．如图1，直角
梯形ABCD中，
，
E，F分别为边AD和BC上的点，且EF//AB，AD=2AE=2AB=4FC=4将四边形EFCD沿EF折起（如图2），使AD=AE.
（Ⅰ）求证：BC//平面DAE；
（Ⅱ）求四棱锥D—AEFB的体积；
（Ⅲ）求面CBD与面DAE所成锐二面角的余弦值.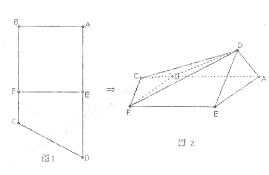
的所有直线中距离原点最远的直线方程是什么？
截得线段的中点是
点，当
，
时，求此直线方程。
并且和两个坐标轴围成的三角形的面积是
的直线方程。
作直线
，使它与两坐标轴相交且与两轴所围成的三角形面积为
．
并且在两个坐标轴上的截距的绝对值相等的直线有几条？请求出这些直线的方程。推荐套卷
．如图1，直角梯形ABCD中，，E，F分别为边AD和BC上的点，且EF//AB，AD=2AE=2AB=4FC=4将四边形EFCD沿EF折起（如图2），使AD=AE.
（Ⅰ）求证：BC//平面DAE；
（Ⅱ）求四棱锥D—AEFB的体积；
（Ⅲ）求面CBD与面DAE所成锐二面角的余弦值.
粤公网安备 44130202000953号