甲、乙两篮球运动员 互不影响地在同一位置投球,命中率分别为
互不影响地在同一位置投球,命中率分别为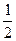 与
与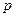 ,且乙投球2次均未命中的概率是
,且乙投球2次均未命中的概率是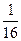 . 求:
. 求:
(1)乙投球的命中率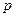 ;
;
(2)甲投球2次,至少命中1次的概率;
(3)若甲、乙二人各投球2次,求两人共命中2次的概率
推荐套卷
甲、乙两篮球运动员 互不影响地在同一位置投球,命中率分别为
互不影响地在同一位置投球,命中率分别为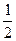 与
与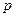 ,且乙投球2次均未命中的概率是
,且乙投球2次均未命中的概率是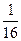 . 求:
. 求:
(1)乙投球的命中率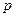 ;
;
(2)甲投球2次,至少命中1次的概率;
(3)若甲、乙二人各投球2次,求两人共命中2次的概率