已知椭圆 :
: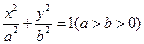 的离心率为
的离心率为 ,且过点
,且过点 ,设椭圆的右准线
,设椭圆的右准线 与
与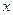 轴的交点为
轴的交点为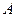 ,椭圆的上顶点为
,椭圆的上顶点为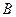 ,直线
,直线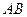 被以原点为圆心的圆
被以原点为圆心的圆 所截得的弦长为
所截得的弦长为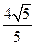 .
.
⑴求椭圆 的方程及圆
的方程及圆 的方程;
的方程;
⑵若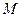 是准线
是准线 上纵坐标为
上纵坐标为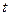 的点,求证:存在一个异于
的点,求证:存在一个异于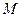 的点
的点 ,对于圆
,对于圆 上任意一点
上任意一点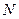 ,有
,有 为定值;且当
为定值;且当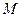 在直线
在直线 上运动时,点
上运动时,点 在一个定圆上.
在一个定圆上.
推荐套卷
已知椭圆 :
: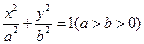 的离心率为
的离心率为 ,且过点
,且过点 ,设椭圆的右准线
,设椭圆的右准线 与
与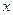 轴的交点为
轴的交点为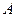 ,椭圆的上顶点为
,椭圆的上顶点为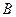 ,直线
,直线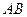 被以原点为圆心的圆
被以原点为圆心的圆 所截得的弦长为
所截得的弦长为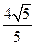 .
.
⑴求椭圆 的方程及圆
的方程及圆 的方程;
的方程;
⑵若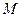 是准线
是准线 上纵坐标为
上纵坐标为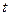 的点,求证:存在一个异于
的点,求证:存在一个异于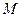 的点
的点 ,对于圆
,对于圆 上任意一点
上任意一点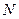 ,有
,有 为定值;且当
为定值;且当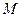 在直线
在直线 上运动时,点
上运动时,点 在一个定圆上.
在一个定圆上.