某大学毕业生参加一个公司的招聘考试，考试分笔试和面试两个环节，笔试有A、B两个题目，该学生答对A、B两题的概率分别为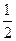
和
，两题全部答对方可过入面试，面试要回答甲、乙两个题目，该学生答对这两个题目的概率均为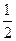，至少答对一题即可被聘用（假设每个环节的每个题目回答正确与否是相互独立的）
（1）求该学生被公司聘用的概率；
（2）设该学生答对题目的个数为
，求的分布列和数学期望.
相关试题
，
.
的解析式；
的方程
，
时，对任意
总有
成立，求
的取值范围.
的函数
是奇函数.
的值
的单调性；
，不等式
恒成立，求实数
的取值范围.
满足
，且
。
时，方程
有解，求实数
的取值范围；
，
,求
的最大值.
,若
，求实数
的取值范围。
。
在
上的最小值；
，
恒成立，求实数
的取值范围.推荐套卷
某大学毕业生参加一个公司的招聘考试，考试分笔试和面试两个环节，笔试有A、B两个题目，该学生答对A、B两题的概率分别为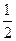和，两题全部答对方可过入面试，面试要回答甲、乙两个题目，该学生答对这两个题目的概率均为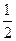，至少答对一题即可被聘用（假设每个环节的每个题目回答正确与否是相互独立的）
（1）求该学生被公司聘用的概率；
（2）设该学生答对题目的个数为，求的分布列和数学期望.
粤公网安备 44130202000953号