一条笔直的公路垂直交叉于十字路口A处,甲小组乘一辆汽车,约定向东为正,从A地出发到收工时,行走记录为(单位:千米):+15,-2,+5,-1,+10,-3,-2,+12,+4,-5,+6.同时,乙小组也从A地出发,沿南北方向的公路检修线路,约定向北为正,行走记录为:-17,+9,-2,+8,+6,+9,-5,-1,+4,-7,-8.
(1)分别计算收工时,甲、乙两组各在检修站A地的哪一边,分别距A地多远?
(2)若每千米汽车耗油2升,求出发到收工时两组各耗油多少升?
相关知识点
推荐套卷
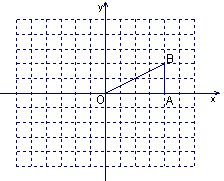
 关于点O成中心对称的
关于点O成中心对称的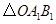 ,并写出点B1的坐标;
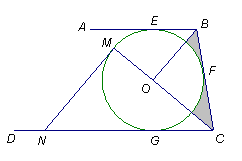
,并写出点B1的坐标; 的两条弦, 且
的两条弦, 且 .求证:
.求证: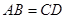 .
.
 粤公网安备 44130202000953号
粤公网安备 44130202000953号