某工厂,加负责加工A型零件,乙负责加工B型零件。已知甲加工60个A型零件所用时间和乙加工80个B型零件所用时间相同,每天甲、乙两人共加工两种零件35个,设甲每天加工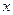 个A型零件.
个A型零件.
(1)求甲、乙每天各加工多少个零件;(列分式方程 解应用题)
解应用题)
(2)根据市场预测估计,加工A型零件所获得的利润为m元/ 件(3≤m≤5) ,加工B型零件所获得的利润每件比A型少1元.求每天甲、乙加工的零件所获得的总利润
,加工B型零件所获得的利润每件比A型少1元.求每天甲、乙加工的零件所获得的总利润 (元)与m(元/件)的函数关系式,并求总利润
(元)与m(元/件)的函数关系式,并求总利润 的最大值、最小值.
的最大值、最小值.
相关知识点
推荐套卷
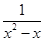 ,
,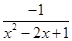 ;
;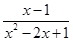 ;
;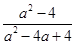 ;
; 时,求
时,求 的值.
的值.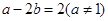 ,求
,求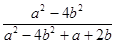 -a2+4ab-4b2的值.
-a2+4ab-4b2的值. 粤公网安备 44130202000953号
粤公网安备 44130202000953号