某单位建造一间地面面积为12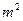
的背面靠墙的矩形小屋，房屋正面的造价为12
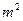00元/，房屋侧面造价为800元/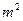，屋顶
的总造价为5800元，如果墙面高为3m，且不计房屋背面费用，问怎样设计房屋能使得总造价最低，最低造价为多少元？
相关试题
满足
,且
是纯虚数,求
.
的方程
有实数根
．
，
满足
，求
有最小值并求出最小值．
是复数，
与
均为实数，且复数
在复平面上对应的点在第一象限，求实数
的取值范围．
为坐标原点，已知向量
，
分别对应复数
，且
，
，
．若
可以与任意实数比较大小，求
为何值时，复数
．推荐套卷
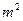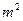某单位建造一间地面面积为12的背面靠墙的矩形小屋，房屋正面的造价为1200元/，房屋侧面造价为800元/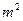，屋顶的总造价为5800元，如果墙面高为3m，且不计房屋背面费用，问怎样设计房屋能使得总造价最低，最低造价为多少元？
粤公网安备 44130202000953号