某校要用三辆汽车从新校区把教职工接到老校区,已知从新校区到老校区有两条公路,汽车走公路①堵车的概率为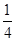 ,不堵车的概率为
,不堵车的概率为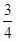 ;汽车走公路②堵车的概率为
;汽车走公路②堵车的概率为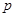 ,不堵车的概率为
,不堵车的概率为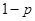 .若甲、乙两辆汽车走公路①,丙汽车由于其他原因走公路②,且三辆车是否堵车相互之间没有影响
.若甲、乙两辆汽车走公路①,丙汽车由于其他原因走公路②,且三辆车是否堵车相互之间没有影响 . (Ⅰ)若三辆汽车中恰有一辆汽车被堵
. (Ⅰ)若三辆汽车中恰有一辆汽车被堵 的概率为
的概率为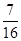 ,求走公路②堵车的概率;
,求走公路②堵车的概率;
(Ⅱ)在(Ⅰ)的条件下,求三辆汽车中被堵车辆的个数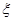 的分布列和数学期望。
的分布列和数学期望。
推荐套卷
某校要用三辆汽车从新校区把教职工接到老校区,已知从新校区到老校区有两条公路,汽车走公路①堵车的概率为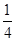 ,不堵车的概率为
,不堵车的概率为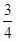 ;汽车走公路②堵车的概率为
;汽车走公路②堵车的概率为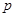 ,不堵车的概率为
,不堵车的概率为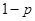 .若甲、乙两辆汽车走公路①,丙汽车由于其他原因走公路②,且三辆车是否堵车相互之间没有影响
.若甲、乙两辆汽车走公路①,丙汽车由于其他原因走公路②,且三辆车是否堵车相互之间没有影响 . (Ⅰ)若三辆汽车中恰有一辆汽车被堵
. (Ⅰ)若三辆汽车中恰有一辆汽车被堵 的概率为
的概率为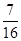 ,求走公路②堵车的概率;
,求走公路②堵车的概率;
(Ⅱ)在(Ⅰ)的条件下,求三辆汽车中被堵车辆的个数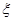 的分布列和数学期望。
的分布列和数学期望。