下列四个命题中,真命题的序号有  (写出所有真命题的序号).
(写出所有真命题的序号).
①两个相互垂直的平面,一个平面内的任意一直线必垂直于另一平面内的无数条直线.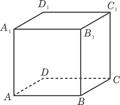 ②圆x2+y2+4x+2y+1=0与直线y=
②圆x2+y2+4x+2y+1=0与直线y= 相交,所得弦长为2.
相交,所得弦长为2.
③若sin( +
+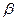 )=
)= ,si
,si n(
n( -
-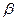 )=
)=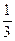 ,则tan
,则tan cot
cot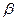 =5.
=5.
④如图,已知正方体ABCD- A1B1C1D1,P为底面ABCD内一动点,
P到平面AA1D1D的距离与到直线CC1的距离相等,则P点的轨迹是抛物线的一部分.
相关知识点
推荐套卷
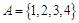 ,
,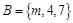 ,若
,若 ,则
,则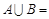 .
. 是偶函数,则
是偶函数,则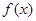 的递减区间是.
的递减区间是.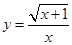 的定义域为_________.
的定义域为_________.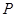 是一个数集,且至少含有两个数,若对任意
是一个数集,且至少含有两个数,若对任意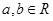 ,都有
,都有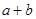 、
、 ,
,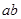 、
、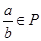 (除数
(除数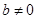 ),则称
),则称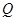 是数域;数集
是数域;数集 也是数域.有下列命题:①数域必含有
也是数域.有下列命题:①数域必含有 ,
,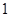 两个数;②整数集是数域;③若有理数集
两个数;②整数集是数域;③若有理数集 ,则数集
,则数集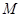 必为数域;④数域必为无限集;⑤存在无穷多个数域.其中正确的命题的序号是_______.(把你认为正确的命题的序号填填上)
必为数域;④数域必为无限集;⑤存在无穷多个数域.其中正确的命题的序号是_______.(把你认为正确的命题的序号填填上)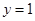 与函数
与函数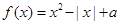 的图象有两个交点,则实数
的图象有两个交点,则实数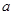 的取值范围是_________.
的取值范围是_________. 粤公网安备 44130202000953号
粤公网安备 44130202000953号