(本题满分10分)
在等边△ABC中，D、E分别在AC、BC上，且AD=CE=nAC，连AE、BD相交于P，过B作BQ⊥AE于点Q，连CP.
(1)∠BPQ=______,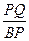
=____
(2)若BP⊥CP，求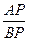
；
(3)当n=_____时，BP⊥CP?
相关试题
相关知识点
推荐套卷
(本题满分10分)
在等边△ABC中，D、E分别在AC、BC上，且AD=CE=nAC，连AE、BD相交于P，过B作BQ⊥AE于点Q，连CP.
(1)∠BPQ=______,=____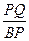
(2)若BP⊥CP，求；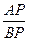
(3)当n=_____时，BP⊥CP?
粤公网安备 44130202000953号