（本题8分）
如图，已知抛物线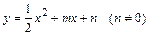
与直线y=x交于A、B两点，与y轴交于点C，OA＝OB，BC∥x轴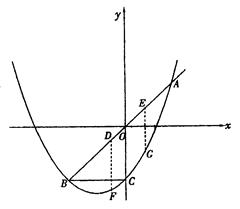
(1)求抛物线的解析式．
(2)设D、E是线段AB上异于A、B的两个动点(点E在点D的上方)，DE＝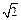
，过D、E两点分别作y轴的平行线，交抛物线于F、G，若设D点的横坐标为x，四边形DEGF的面积为y，求x与y之间的关系式，写出自变量x的取值范围，并回答x为何值时，y有最大值．
相关试题
，并且使点P到
的两边的距离相等，并说明你的理由．
相关知识点
推荐套卷
（本题8分）
如图，已知抛物线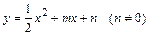与直线y=x交于A、B两点，与y轴交于点C，OA＝OB，BC∥x轴
(1)求抛物线的解析式．
(2)设D、E是线段AB上异于A、B的两个动点(点E在点D的上方)，DE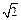＝，过D、E两点分别作y轴的平行线，交抛物线于F、G，若设D点的横坐标为x，四边形DEGF的面积为y，求x与y之间的关系式，写出自变量x的取值范围，并回答x为何值时，y有最大值．
粤公网安备 44130202000953号