(本小题满分8分)
如图是一个可以自由转动的转盘,自由转动这个转盘四次后得到4个数字,分别填在各个空格内(顺序自定),组成一个数.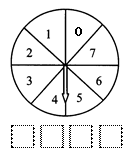
(1)你认为有可能得到的最小的数是多少?
(2)利用这个转盘,可能得到的最大的四位数是多少?可能得到的最小的四位数是多少?它们出现的可能性谁大?
相关知识点
推荐套卷
(本小题满分8分)
如图是一个可以自由转动的转盘,自由转动这个转盘四次后得到4个数字,分别填在各个空格内(顺序自定),组成一个数.
(1)你认为有可能得到的最小的数是多少?
(2)利用这个转盘,可能得到的最大的四位数是多少?可能得到的最小的四位数是多少?它们出现的可能性谁大?