（本小题满分12分）
某单位有三辆汽车参加某种事故保险，年初向保险公司缴纳每辆900元的保险金，对在一年内发生此种事故的每辆汽车，单位可获9000元的赔偿（假设每辆车每年最多只赔偿一次），设这三辆车在一年内发生此种事故的概率分别为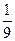
、
、
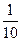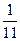，且各车是否发生事故相互独立，求一年内该单位在此保险中：
（Ⅰ）获赔的概率；
（Ⅱ）获赔金额ξ的分布列与期望．
相关试题
,则该二面角的大小为 .
,2),则m= .推荐套卷
（本小题满分12分）
某单位有三辆汽车参加某种事故保险，年初向保险公司缴纳每辆900元的保险金，对在一年内发生此种事故的每辆汽车，单位可获9000元的赔偿（假设每辆车每年最多只赔偿一次），设这三辆车在一年内发生此种事故的概率分别为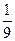、、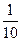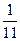，且各车是否发生事故相互独立，求一年内该单位在此保险中：
（Ⅰ）获赔的概率；
（Ⅱ）获赔金额ξ的分布列与期望．
粤公网安备 44130202000953号