设函数f(x)＝xn（n≥2，n∈N*）
（1）若Fn(x)＝f(x－a)＋f(b－x)（0＜a＜x＜b），求Fn(x)的取值范围；
（2）若Fn(x)＝f(x－b)－f(x－a)，对任意n≥a (2≥a＞b＞0)，
证明：F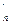
(n)≥n(a－b)(n－b)n-2。
相关试题
满足，
。（1）求
和
，求数列
的前n项和
中，角
、
、
对的边分别为
、
、
，且满足:
, 
的两根。
，求
是等差数列，且
为
中，已知
，
是
边上的一点，
。求AB的长。
中，
，求
和
。推荐套卷
设函数f(x)＝xn（n≥2，n∈N*）
（1）若Fn(x)＝f(x－a)＋f(b－x)（0＜a＜x＜b），求Fn(x)的取值范围；
（2）若Fn(x)＝f(x－b)－f(x－a)，对任意n≥a (2≥a＞b＞0)，
证明：F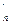(n)≥n(a－b)(n－b)n-2。
粤公网安备 44130202000953号