(本小题满分9分)
如图所示，抛物线
与x轴交于A、B两点，直线BD的函数表达式为
，抛物线的对称轴l与直线BD交于点C、与x轴交于点E．
⑴求A、B、C三个点的坐标．
⑵点P为线段AB上的一个动点（与点A、点B不重合），以点A为圆心、以AP为半径的圆弧与线段AC交于点M，以点B为圆心、以BP为半径的圆弧与线段BC交于点N，分别连接AN、BM、MN．
①求证：AN=BM．
②在点P运动的过程中，四边形AMNB的面积有最大值还是有最小值？并求出该最大值或最小值.
相关试题
在“5.12大地震”灾民安置工作中，某企业接到一批生产甲种板材24000
和乙种板材12000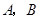的任务．（1）已知该企业安排140人生产这两种板材，每人每天能生产甲种板材30或乙种板材20．问：应分别安排多少人生产甲种板材和乙种板材，才能确保他们用相同的时间完成各自的生产任务？
（2）某灾民安置点计划用该企业生产的这批板材搭建
两种型号的板房共400间，在搭建过程中，按实际需要调运这两种板材．已知建一间
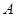型板房和一间
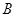型板房所需板材及能安置的人数如下表所示：
| 板房型号 |
甲种板材 |
乙种板材 |
安置人数 |
| 型板房 |
54 |
26 |
5 |
| 型板房 |
78 |
41 |
8 |
问：这400间板房最多能安置多少灾民？
如图，一次函数y＝kx＋b与反比例函数y＝
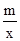的图象交于A（4，6），B（－6，n）两点．（1）求一次函数与反比例函数的解析式；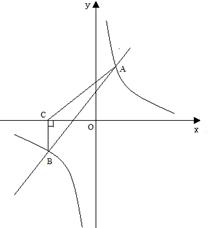
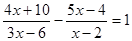
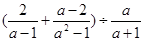（2）根据所给条件，请直接写出不等式kx＋b＜的解集______________；
（3）过点B作BC⊥x轴，垂足为C，求S△ABC． 
，其中
相关知识点
推荐套卷
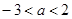
粤公网安备 44130202000953号