（本小题满分12分）假设某奶粉是经过A、B、C三道工序加工而成的，A、B、C工序的产品合格率分别为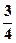
、
、
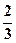。已知每道工序的加工都相互独立，三道工序加工的产品都为合格时产品为一等品；有两道合格为二等品；其它的为废品，不进入市场。
（Ⅰ）正式生产前先试生产2袋奶粉，求这2袋奶粉都为废品的概率；
（Ⅱ）设
为加工工序中产品合格的次数，求的分布列和数学期望。
是定义在
上的偶函数，且
时，
．
，
；
，求
的取值范围．
，求函数
的最大值和最小值．
，
．
；
，求实数
的取值集合．
；
．
经过点
，离心率为
，过点
的直线
与椭圆
交于不同的两点
，
．
的取值范围．推荐套卷
（本小题满分12分）假设某奶粉是经过A、B、C三道工序加工而成的，A、B、C工序的产品合格率分别为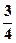、、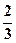。已知每道工序的加工都相互独立，三道工序加工的产品都为合格时产品为一等品；有两道合格为二等品；其它的为废品，不进入市场。
（Ⅰ）正式生产前先试生产2袋奶粉，求这2袋奶粉都为废品的概率；
（Ⅱ）设为加工工序中产品合格的次数，求的分布列和数学期望。
粤公网安备 44130202000953号