(10分) 如图，在方格纸（每个小正方形边长为1）中，先把梯形ABCD向左平移6个单位长度得到梯形A1B1C1D1．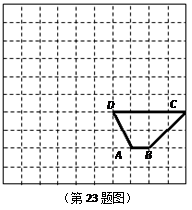
（1）请你在方格纸中画出梯形A1B1C1D1 ；
（2）以点C1为旋转中心，把 (1) 中画出的梯形绕点C1顺时针方向旋转
得到梯形A2B2C2D2，请你画出梯形A2B2C2D2．
d中，已知S2=5，S4=14，求S6的值.
相关知识点
推荐套卷
(10分) 如图，在方格纸（每个小正方形边长为1）中，先把梯形ABCD向左平移6个单位长度得到梯形A1B1C1D1．
（1）请你在方格纸中画出梯形A1B1C1D1 ；
（2）以点C1为旋转中心，把 (1) 中画出的梯形绕点C1顺时针方向旋转得到梯形A2B2C2D2，请你画出梯形A2B2C2D2．
粤公网安备 44130202000953号