(本小题满分13分)有一座大桥既是交通拥挤地段,又是事故多发地段,为了保证安全,交通部门规定。大桥上的车距 与车速
与车速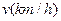 和车长
和车长 的关系满足:
的关系满足: (
(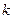 为正的常数),假定车身长为
为正的常数),假定车身长为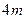 ,当车速为
,当车速为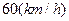 时,车距为2.66个车身长。
时,车距为2.66个车身长。
(1)写出车距 关于车速
关于车速 的函数关系式;
的函数关系式;
(2)应规定怎样的车速,才能使大桥上每小时通过的车辆最多?
推荐套卷
(本小题满分13分)有一座大桥既是交通拥挤地段,又是事故多发地段,为了保证安全,交通部门规定。大桥上的车距 与车速
与车速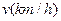 和车长
和车长 的关系满足:
的关系满足: (
(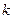 为正的常数),假定车身长为
为正的常数),假定车身长为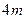 ,当车速为
,当车速为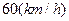 时,车距为2.66个车身长。
时,车距为2.66个车身长。
(1)写出车距 关于车速
关于车速 的函数关系式;
的函数关系式;
(2)应规定怎样的车速,才能使大桥上每小时通过的车辆最多?