(本小题满分12分)
某市居民自来水收费标准如下:每户每月用水不超过4吨时每吨为1.80元,当用水超过4吨时,超过部分每吨3.00元,某月甲、乙两户共交水费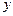 元,已知甲、乙两用户 该月用水量分别为
元,已知甲、乙两用户 该月用水量分别为 (吨)。
(吨)。
(1)求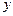 关于
关于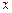 的函数;
的函数;
(2)若甲、乙两户该月共交水费26.4元,分别求出甲、乙两户该月的用水量和水费。(精确到0.1)
推荐套卷
(本小题满分12分)
某市居民自来水收费标准如下:每户每月用水不超过4吨时每吨为1.80元,当用水超过4吨时,超过部分每吨3.00元,某月甲、乙两户共交水费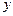 元,已知甲、乙两用户 该月用水量分别为
元,已知甲、乙两用户 该月用水量分别为 (吨)。
(吨)。
(1)求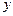 关于
关于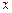 的函数;
的函数;
(2)若甲、乙两户该月共交水费26.4元,分别求出甲、乙两户该月的用水量和水费。(精确到0.1)