(本小题满分12分)在某次足球比赛中,甲、乙、丙三队进行单循环赛(即每两队比赛一场),共赛三场,每场比赛胜者得1分,输者得0分,没有平局;在每一场比赛中,甲胜乙的概率为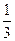 ,甲胜丙的概率为
,甲胜丙的概率为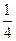 ,乙胜丙的概率为
,乙胜丙的概率为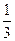 .
.
(Ⅰ)求甲获得小组第一且丙获得小组第二的概率;
(Ⅱ)求三队得分相同的概率;
(Ⅲ)求甲不是小组第一的概率.
推荐套卷
(本小题满分12分)在某次足球比赛中,甲、乙、丙三队进行单循环赛(即每两队比赛一场),共赛三场,每场比赛胜者得1分,输者得0分,没有平局;在每一场比赛中,甲胜乙的概率为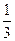 ,甲胜丙的概率为
,甲胜丙的概率为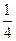 ,乙胜丙的概率为
,乙胜丙的概率为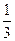 .
.
(Ⅰ)求甲获得小组第一且丙获得小组第二的概率;
(Ⅱ)求三队得分相同的概率;
(Ⅲ)求甲不是小组第一的概率.