设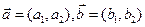 ,定义一种向量运算
,定义一种向量运算 .已知
.已知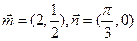 ,点
,点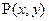 在
在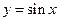 的图像上运动,点Q在
的图像上运动,点Q在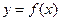 的图像上运动且满足
的图像上运动且满足 (其中O为坐标原点),则
(其中O为坐标原点),则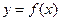 的最大值A及最小正周期T分别为( )
的最大值A及最小正周期T分别为( )
A.2,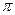 |
B.2,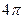  |
C.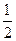 , ,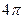 |
D.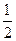 , ,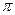 |
推荐套卷
设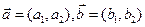 ,定义一种向量运算
,定义一种向量运算 .已知
.已知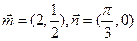 ,点
,点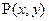 在
在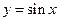 的图像上运动,点Q在
的图像上运动,点Q在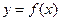 的图像上运动且满足
的图像上运动且满足 (其中O为坐标原点),则
(其中O为坐标原点),则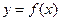 的最大值A及最小正周期T分别为( )
的最大值A及最小正周期T分别为( )
A.2,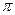 |
B.2,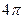  |
C.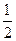 , ,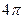 |
D.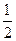 , ,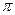 |