(理)命题“若两个正实数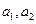 满足
满足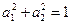 ,那么
,那么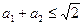 。”
。”
证明如下:构造函数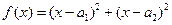 ,因为对一切实数
,因为对一切实数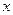 ,恒有
,恒有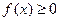 ,
,
又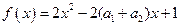 ,从而得
,从而得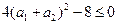 ,所以
,所以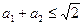 。
。
根据上述证明方法,若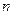 个正实数满足
个正实数满足 时,你可以构造函数
时,你可以构造函数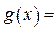 _______ ,进一步能得到的结论为 ______________ (不必证明).
_______ ,进一步能得到的结论为 ______________ (不必证明).
相关知识点
推荐套卷
(理)命题“若两个正实数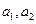 满足
满足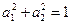 ,那么
,那么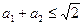 。”
。”
证明如下:构造函数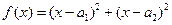 ,因为对一切实数
,因为对一切实数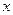 ,恒有
,恒有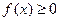 ,
,
又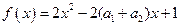 ,从而得
,从而得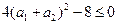 ,所以
,所以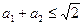 。
。
根据上述证明方法,若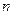 个正实数满足
个正实数满足 时,你可以构造函数
时,你可以构造函数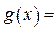 _______ ,进一步能得到的结论为 ______________ (不必证明).
_______ ,进一步能得到的结论为 ______________ (不必证明).