(本题10分)有甲、乙两种商品,经营销售这两种商品所能获得的利润依次是P和Q(万元),它们与投入的资金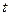 (万元)的关系满足公式P=
(万元)的关系满足公式P=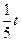 ,Q=
,Q=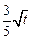 ,现将3万元资金投入经营甲、乙两种商品,设投入乙的资金为x万元,获得的总利润为y(万元)
,现将3万元资金投入经营甲、乙两种商品,设投入乙的资金为x万元,获得的总利润为y(万元)
(1)用x表示y,并指出函数的定义城
(2)当x为何值时,y有最大值,并求出这个最大值
推荐套卷
(本题10分)有甲、乙两种商品,经营销售这两种商品所能获得的利润依次是P和Q(万元),它们与投入的资金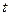 (万元)的关系满足公式P=
(万元)的关系满足公式P=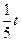 ,Q=
,Q=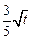 ,现将3万元资金投入经营甲、乙两种商品,设投入乙的资金为x万元,获得的总利润为y(万元)
,现将3万元资金投入经营甲、乙两种商品,设投入乙的资金为x万元,获得的总利润为y(万元)
(1)用x表示y,并指出函数的定义城
(2)当x为何值时,y有最大值,并求出这个最大值