(本小题满分16分)
已知f (x)、g(x)都是定义在R上的函数,如果存在实数m、n使得h (x) = m f(x)+ng(x),那么称h (x)为f (x)、g(x)在R上生成的一个函数.
设f (x)=x2+ax,g(x)=x+b(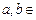 R),
R),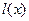 =2x2+3x-1,h (x)为f (x)、g(x)在R上生成的一个二次函数.
=2x2+3x-1,h (x)为f (x)、g(x)在R上生成的一个二次函数.
(1)设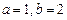 ,若h (x)为偶函数,求
,若h (x)为偶函数,求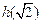 ;
;
(2)设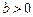 ,若h (x)同时也是g(x)、l(x) 在R上生成的一个函数,求a+b的最小值;
,若h (x)同时也是g(x)、l(x) 在R上生成的一个函数,求a+b的最小值;
推荐套卷
(本小题满分16分)
已知f (x)、g(x)都是定义在R上的函数,如果存在实数m、n使得h (x) = m f(x)+ng(x),那么称h (x)为f (x)、g(x)在R上生成的一个函数.
设f (x)=x2+ax,g(x)=x+b(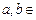 R),
R),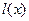 =2x2+3x-1,h (x)为f (x)、g(x)在R上生成的一个二次函数.
=2x2+3x-1,h (x)为f (x)、g(x)在R上生成的一个二次函数.
(1)设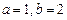 ,若h (x)为偶函数,求
,若h (x)为偶函数,求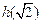 ;
;
(2)设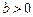 ,若h (x)同时也是g(x)、l(x) 在R上生成的一个函数,求a+b的最小值;
,若h (x)同时也是g(x)、l(x) 在R上生成的一个函数,求a+b的最小值;