(本小题满分12分)
某校举办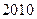 年上海世博会知识竞赛,从参赛的高一、高二学生中各抽
年上海世博会知识竞赛,从参赛的高一、高二学生中各抽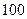 人的成绩作
人的成绩作
 |
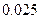 |
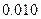 |
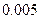 |
 |
 |
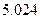 |
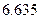 |
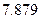 |
 |
为样本,其结果如下表:
参考数据:
| |
高一 |
高二 |
合计 |
| 合格人数 |
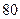 |
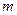 |
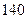 |
| 不合格人数 |
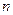 |
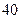 |
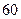 |
| 合计 |
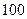 |
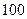 |
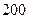 |
(Ⅰ)求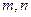 的值;
的值;
(Ⅱ)你有多大的把握认为“高一、高二两个年级这次世博会知识竞赛的成绩有差异”.
推荐套卷
 ,规定数列
,规定数列 为数列
为数列 ;一般地,规定
;一般地,规定 为
为 阶差分数列,其中
阶差分数列,其中 ,且
,且 .
. ,试证明
,试证明 ,且满足
,且满足 ,求数列
,求数列 及
及 是否存在最小值,若存在求出其最小值,若不存在说明理由.
是否存在最小值,若存在求出其最小值,若不存在说明理由. 的前
的前 项和为
项和为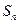 ,且满足
,且满足 (
( 1)求数列
1)求数列 满足
满足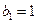 ,且
,且 ,求数列
,求数列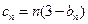 ,求数列
,求数列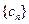 的前
的前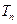 .
.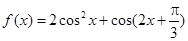
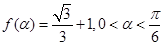 ,求
,求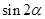 的值;
的值;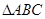 中,
中, ,
,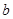 ,
,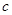 分别是角
分别是角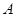 ,
, ,
, 的对边;若
的对边;若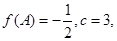
 ,求
,求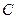 在城
在城 的南偏西
的南偏西 的方向上,由
的方向上,由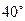 ,在
,在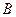 处,有一人正沿公路向
处,有一人正沿公路向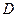 处,此时
处,此时 公里,问此人还需要走多少公里到达
公里,问此人还需要走多少公里到达
 中,
中,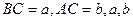 是方程
是方程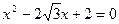 的两个根,且
的两个根,且
 的长度.
的长度. 粤公网安备 44130202000953号
粤公网安备 44130202000953号