（本小题满分10分）
将一枚硬币连续抛掷
次，每次抛掷互不影响. 记正面向上的次数为奇数的概率为
，正面向上的次数为偶数的概率为
.
（Ⅰ）若该硬币均匀，试求与；
（Ⅱ）若该硬币有暇疵，且每次正面向上的概率为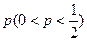
，试比较与的大小.
相关试题
中，
平面
，
是边长为
的等边三角形，
为
边中点，且
．
平面
平面
；
的体积．
中，已知
，
的值；
，求
。
时，求函数
的定义域；
，试求
的取值范围．
经过点
,倾斜角
，
相交与两点
，求点
到
中的两条角平分线
和
相交于
，
，
在
上，且
。
四点共圆；
。
推荐套卷
（本小题满分10分）
将一枚硬币连续抛掷次，每次抛掷互不影响. 记正面向上的次数为奇数的概率为，正面向上的次数为偶数的概率为.
（Ⅰ）若该硬币均匀，试求与；
（Ⅱ）若该硬币有暇疵，且每次正面向上的概率为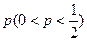，试比较与的大小.
粤公网安备 44130202000953号