(本小题满分14分)
已知椭圆 的焦点F与抛物线C:
的焦点F与抛物线C: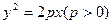 的焦点关于直线x-y=0
的焦点关于直线x-y=0
对称.
(Ⅰ)求抛物线的方程;
(Ⅱ)已知定点A(a,b),B(-a,0)(ab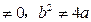 ),M是抛物线C上的点,设直线AM,
),M是抛物线C上的点,设直线AM,
BM与抛物线的另一交点为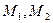 .求证:当M点在抛物线上变动时(只要
.求证:当M点在抛物线上变动时(只要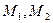 存在
存在
且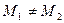 )直线
)直线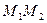 恒过一定点,并求出这个定点的坐标.
恒过一定点,并求出这个定点的坐标.
相关知识点
推荐套卷
(本小题满分14分)
已知椭圆 的焦点F与抛物线C:
的焦点F与抛物线C: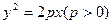 的焦点关于直线x-y=0
的焦点关于直线x-y=0
对称.
(Ⅰ)求抛物线的方程;
(Ⅱ)已知定点A(a,b),B(-a,0)(ab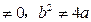 ),M是抛物线C上的点,设直线AM,
),M是抛物线C上的点,设直线AM,
BM与抛物线的另一交点为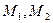 .求证:当M点在抛物线上变动时(只要
.求证:当M点在抛物线上变动时(只要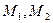 存在
存在
且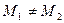 )直线
)直线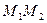 恒过一定点,并求出这个定点的坐标.
恒过一定点,并求出这个定点的坐标.