(请考生在下面甲、乙两题中任选一题做答,如果多做,则按所做的甲题计分)
甲题:
⑴若关于 的不等式
的不等式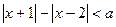 的解集不是空集,求实数
的解集不是空集,求实数 的取值范围;
的取值范围;
⑵已知实数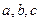 ,满足
,满足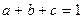 ,求
,求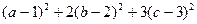 最小值.
最小值.
乙题:
已知曲线C的极坐标方程是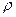 =4cos
=4cos 。以极点为平面直角坐标系的原点,极轴为
。以极点为平面直角坐标系的原点,极轴为 轴的正半轴,建立平面直角坐标系,直线
轴的正半轴,建立平面直角坐标系,直线 的参数方程是
的参数方程是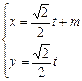 (
(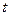 是参数)。
是参数)。
⑴将曲线C的极坐标方程化成直角坐标方程并把直线 的参数方程转化为普通方程;
的参数方程转化为普通方程;
⑵若过定点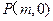 的直线
的直线 与曲线C相交于A、B两点,且
与曲线C相交于A、B两点,且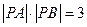 ,试求实数
,试求实数 的值。
的值。
推荐套卷
(请考生在下面甲、乙两题中任选一题做答,如果多做,则按所做的甲题计分)
甲题:
⑴若关于 的不等式
的不等式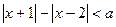 的解集不是空集,求实数
的解集不是空集,求实数 的取值范围;
的取值范围;
⑵已知实数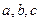 ,满足
,满足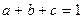 ,求
,求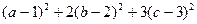 最小值.
最小值.
乙题:
已知曲线C的极坐标方程是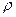 =4cos
=4cos 。以极点为平面直角坐标系的原点,极轴为
。以极点为平面直角坐标系的原点,极轴为 轴的正半轴,建立平面直角坐标系,直线
轴的正半轴,建立平面直角坐标系,直线 的参数方程是
的参数方程是 (
(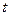 是参数)。
是参数)。
⑴将曲线C的极坐标方程化成直角坐标方程并把直线 的参数方程转化为普通方程;
的参数方程转化为普通方程;
⑵若过定点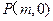 的直线
的直线 与曲线C相交于A、B两点,且
与曲线C相交于A、B两点,且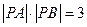 ,试求实数
,试求实数 的值。
的值。