有n2（n≥4）个正数，排成n×n矩阵（n行n列的数表），其中每一行的数成等差数列，每一列的数成等比数列，并且所有公比都相等，且满足a24＝1，a42＝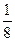
，a43＝
，
求：（1）公比q；
（2）用k表示a4k；
（3）求a11＋a22＋a33＋…＋ann的值。
相关试题
是定义在
上的奇函数，且
在
.
,其中
的值；
的值域．
时，函数
的最小值为
，求实数
的值．
，
, M为AB中点，N为BD靠近B的三等分点.
，
；
．
，求k的值；
，求m的值.推荐套卷
有n2（n≥4）个正数，排成n×n矩阵（n行n列的数表），其中每一行的数成等差数列，每一列的数成等比数列，并且所有公比都相等，且满足a24＝1，a42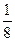＝，a43＝，
求：（1）公比q；
（2）用k表示a4k；
（3）求a11＋a22＋a33＋…＋ann的值。
粤公网安备 44130202000953号