
已知双曲线 的离心率为e,右顶点为A,左、右焦点分别为
的离心率为e,右顶点为A,左、右焦点分别为 、
、 ,点E为右准线上的动点,
,点E为右准线上的动点, 的最大值为
的最大值为 .
.
(1)若双曲线的左焦点为 ,一条渐近线的方程为
,一条渐近线的方程为 ,求双曲线的方程;
,求双曲线的方程;
(2)求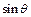 (用
(用 表示);
表示);
(3)如图,如果直线l与双曲线的交点为P、Q,与两条渐近线的交点为 、
、 ,O为坐标原点,求证:
,O为坐标原点,求证:
相关知识点
推荐套卷

已知双曲线 的离心率为e,右顶点为A,左、右焦点分别为
的离心率为e,右顶点为A,左、右焦点分别为 、
、 ,点E为右准线上的动点,
,点E为右准线上的动点, 的最大值为
的最大值为 .
.
(1)若双曲线的左焦点为 ,一条渐近线的方程为
,一条渐近线的方程为 ,求双曲线的方程;
,求双曲线的方程;
(2)求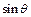 (用
(用 表示);
表示);
(3)如图,如果直线l与双曲线的交点为P、Q,与两条渐近线的交点为 、
、 ,O为坐标原点,求证:
,O为坐标原点,求证: