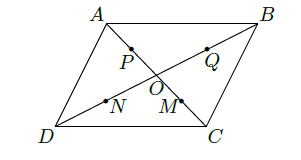
在平行四边形 中, 是 与 的交点, 分别是线段 的中点,在 中任取一点记为 ,在 中任取一点记为 ,设 为满足向量 的点,则在上述的点 组成的集合中的点,落在平行四边形 外(不含边界)的概率为 .
相关知识点
推荐套卷
在平行四边形 中, 是 与 的交点, 分别是线段 的中点,在 中任取一点记为 ,在 中任取一点记为 ,设 为满足向量 的点,则在上述的点 组成的集合中的点,落在平行四边形 外(不含边界)的概率为 .
