某食品厂为了检查一条自动包装流水线的生产情况，随即抽取该流水线上40件产品作为样本算出他们的重量（单位：克）重量的分组区间为
，
，……
，由此得到样本的频率分布直方图，如图所示．
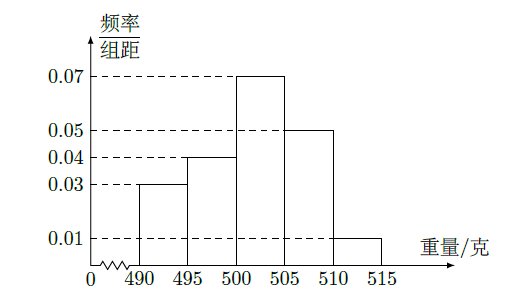
（1）根据频率分布直方图，求重量超过505克的产品数量．
（2）在上述抽取的40件产品中任取2件，设Y为重量超过505克的产品数量，求Y的分布列．
（3）从流水线上任取5件产品，求恰有2件产品合格的重量超过505克的概率．
相关试题
，若点P(1，1)在矩阵A对应的变换作用下得到点P′(0，-8)．二阶矩阵M对应的变换将点(1，－1)与(－2，1)分别变换成点(－1，－1)与(0，－2)．
(1)求矩阵M；
(2)设直线l在变换M作用下得到了直线m：x－y＝4，求l的方程．
，向量α＝
，β＝
.
β在TM作用下的象；
相关知识点
推荐套卷
粤公网安备 44130202000953号