（本小题满分12分）
设椭圆
的离心率
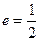，右焦点到直线
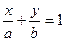的距离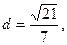
O为坐标原点。
（I）求椭圆C的方程；
（II）过点O作两条互相垂直的射线，与椭圆C分别交于A，B两点，证明点O到直线AB的距离为定值，并求弦AB长度的最小值。
相关试题
的各项均为正数，且
. （1）求数列
，求数列
的前
项和
.
的最小值及对应的x、y值.
的最小值；
，内角
所对的边分别为
，且满足下列三个条件：①
②
③
和边长
的大小； (2) 
)=
, 若
2）=1；
的值；
为R上的单调递增函数推荐套卷
（本小题满分12分）
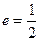设椭圆的离心率，右焦点到直线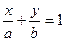的距离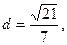O为坐标原点。
（I）求椭圆C的方程；
（II）过点O作两条互相垂直的射线，与椭圆C分别交于A，B两点，证明点O到直线AB的距离为定值，并求弦AB长度的最小值。
粤公网安备 44130202000953号