(本小题满分12分)已知定义在R上的单调函数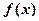 ,存在实数
,存在实数 ,使得对于任意实数
,使得对于任意实数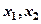 ,总有
,总有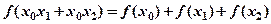 恒成立。
恒成立。
(Ⅰ)求 的值;(Ⅱ)若
的值;(Ⅱ)若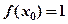 ,且对任意
,且对任意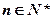 ,有
,有 ,求{an}的通项公式;
,求{an}的通项公式;
(Ⅲ)若数列{bn}满足 ,将数列{bn}的项重新组合成新数列
,将数列{bn}的项重新组合成新数列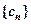 ,具体法则如下:
,具体法则如下: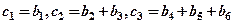 ,……,求证:
,……,求证: 。
。
推荐套卷
(本小题满分12分)已知定义在R上的单调函数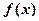 ,存在实数
,存在实数 ,使得对于任意实数
,使得对于任意实数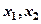 ,总有
,总有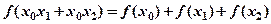 恒成立。
恒成立。
(Ⅰ)求 的值;(Ⅱ)若
的值;(Ⅱ)若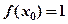 ,且对任意
,且对任意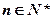 ,有
,有 ,求{an}的通项公式;
,求{an}的通项公式;
(Ⅲ)若数列{bn}满足 ,将数列{bn}的项重新组合成新数列
,将数列{bn}的项重新组合成新数列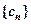 ,具体法则如下:
,具体法则如下: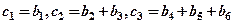 ,……,求证:
,……,求证: 。
。