（本小题满分12分）已知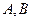
两地的距离是120km．假设汽油的价格是6元/升，以
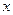km/h（其中
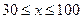）速度行驶时，汽车的耗油率为
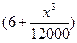L/h，司机每小时的工资是28元．那么最经济的车速是多少？如不考虑其他费用，这次行车的总费用是多少？
，求
.
．
的最小正周期、最小值、最大值；
区间
内的图象．
，且
与
夹角为
。求：
；（2）
的夹角。
．
,求以
为切点的曲线的切线方程；
恒成立，确定实数K的取值范围；
．推荐套卷
（本小题满分12分）已知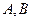两地的距离是120km．假设汽油的价格是6元/升，以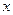km/h（其中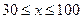）速度行驶时，汽车的耗油率为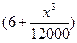L/h，司机每小时的工资是28元．那么最经济的车速是多少？如不考虑其他费用，这次行车的总费用是多少？
粤公网安备 44130202000953号