（本小题共13分）
已知某个几何体的三视图如图（主视图的弧线是半圆），根据图中标出的数据，
（Ⅰ）求这个组合体的体积；
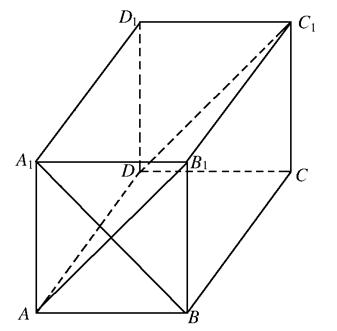
（Ⅱ）若组合体的底部几何体记为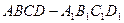
，其中
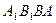为正方形.
（i）求证：
；
（ii）求证：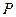
为棱
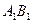上一点，求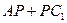
的最小值.
的对称点在单位圆
上，求椭圆的方程
是
的极值点，求
上的最小值和最大值；
上是增函数，求实数
的取值范围
与
；
的反函数
及
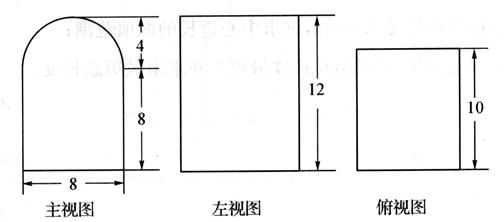
上是增函数推荐套卷
（本小题共13分）
已知某个几何体的三视图如图（主视图的弧线是半圆），根据图中标出的数据，
（Ⅰ）求这个组合体的体积；
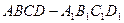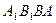（Ⅱ）若组合体的底部几何体记为，其中为正方形.
（i）求证：；
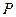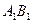（ii）求证：为棱上一点，求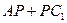的最小值.
粤公网安备 44130202000953号